La moltiplicazione è una delle quattro operazioni di base dell’aritmetica e dà il risultato della combinazione di gruppi di uguali dimensioni.
Anche se ormai con l’utilizzo dei computer e delle calcolatrici si è persa un po’ la pratica nel fare le operazioni, nelle prossime righe scoprirai come si fanno le moltiplicazioni guardando degli esempi pratici che ti aiuteranno a capire questa operazione.
Indice
La moltiplicazione
Nell’immagine qui in basso ci sono dei gelati e come puoi vedere sono divisi in due gruppi ciascuno con 3 gelati. Quindi, per capire il funzionamento della moltiplicazione, devi pensare che ci sono 2 volte 3 gelati o più semplicemente 3 + 3 gelati, quindi un totale di 6. In altre parole, possiamo definire la moltiplicazione come un’addizione ripetuta.

La moltiplicazione è rappresentata dal segno “×”, “*” (asterisco) oppure “·” (punto). Quando moltiplichiamo due numeri, il risultato che otteniamo si chiama “prodotto”, il numero di oggetti in ciascun gruppo è chiamato “moltiplicando” e il numero dei gruppi uguali è chiamato “moltiplicatore”.
Ecco qualche esempio di moltiplicazione:
- 3 × 5 = 5 + 5 + 5 = 15
- 5 × 6 = 6 + 6 + 6 + 6 + 6 = 30
- 4 * 4 = 4 + 4 + 4 + 4 = 16
- 7 x 3 = 3 + 3 + 3 + 3 + 3 + 3 + 3 = 21
Nell’immagine seguente, puoi vedere 4 fiori con 6 ciascuno. Per trovare il numero totale di petali, possiamo moltiplicare il numero totale di fiori per il numero di petali presente in ogni fiore. Quindi, il moltiplicando è 6, il moltiplicatore è 4 e il prodotto è 4 × 6 o 24. Cioè, ci sono 24 petali in tutto.

Moltiplicazioni con la retta numerica
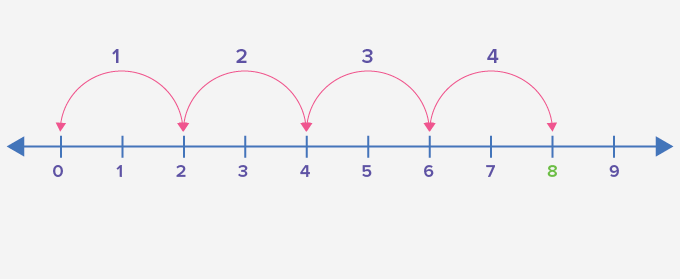
Una moltiplicazione su una retta numerica può essere rappresentata con dei salti di stessa ampiezza. Quindi il numero di salti rappresenterà il moltiplicatore e l’ampiezza dei salti il moltiplicando. Nell’esempio seguente, puoi vedere come rappresentare la moltiplicazione 4 x 2.
Proprietà delle moltiplicazioni
Le proprietà delle moltiplicazioni sono 3.
- Proprietà commutativa: quando moltiplichiamo due numeri, l’ordine non ha importanza. Per i numeri a e b abbiamo che a × b = b × a.
- Proprietà associativa : per i numeri a, b e c si ha che (a × b) × c = a × (b × c).
- Proprietà distributiva : per i numeri a, b e c abbiamo che a × (b + c) = (a × b) + (a × c).
Per quanto riguarda le moltiplicazioni, devi sapere anche che il prodotto di qualsiasi numero moltiplicato per 1 è sempre uguale al numero stesso (782 x 1 = 782). Mentre il risultato di qualsiasi numero moltiplicato per 0 (elemento assorbente) è sempre uguale a 0 (125 x 0 = 0).
Leggi Anche: Come si fanno le divisioni in colonna
Leggi Anche: Colazioni e merende sane per i giorni di scuola


